Расчет средней суммы - это фундаментальная математическая операция, используемая в статистике, финансах и анализе данных. Рассмотрим основные методы вычисления средней величины и их практическое применение.
Содержание
Основные виды средних величин
| Среднее арифметическое | Сумма значений, деленная на их количество |
| Среднее взвешенное | Учитывает значимость каждого элемента |
| Медиана | Серединное значение упорядоченного ряда |
| Мода | Наиболее часто встречающееся значение |
Формула среднего арифметического
Средняя сумма = (x₁ + x₂ + ... + xₙ) / n
где x₁, x₂, ..., xₙ - значения в выборке, n - количество значений
Пошаговый расчет средней суммы
- Соберите все значения для расчета
- Просуммируйте все значения
- Подсчитайте количество значений
- Разделите сумму на количество
- Округлите результат при необходимости
Примеры расчета
| Данные | Расчет | Результат |
| 5, 7, 3 | (5+7+3)/3 | 5 |
| 120, 150, 180 | (120+150+180)/3 | 150 |
Особые случаи расчета
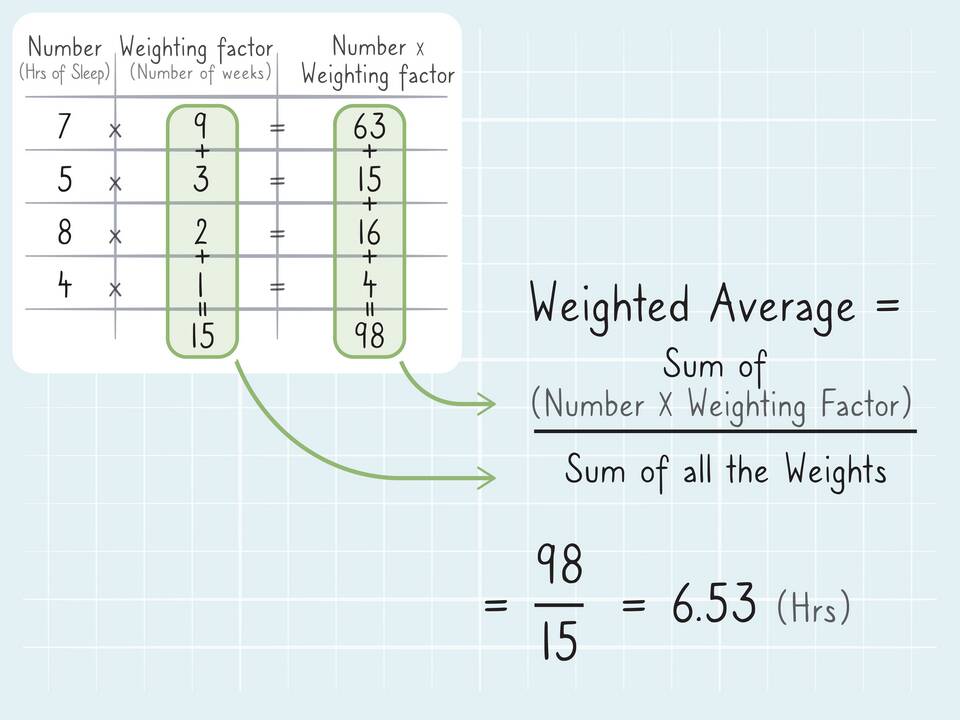
Среднее взвешенное
Средняя сумма = (x₁×w₁ + x₂×w₂ + ... + xₙ×wₙ) / (w₁ + w₂ + ... + wₙ)
где w - весовые коэффициенты
Расчет по сгруппированным данным
- Определите середины интервалов
- Умножьте на частоты
- Суммируйте произведения
- Разделите на общее количество
Применение в различных областях
- Финансы: средний доход, средние расходы
- Статистика: средние показатели
- Экономика: средние цены
- Образование: средний балл
Ограничения и погрешности
| Выбросы | Сильно искажают среднее значение |
| Неоднородные данные | Требуют использования взвешенного среднего |
| Округление | Может привести к потере точности |
Правильный расчет средней суммы требует понимания природы данных и выбора соответствующего метода вычисления. Для сложных случаев рекомендуется использовать специализированное программное обеспечение или статистические методы.